Delaunay Triangulations




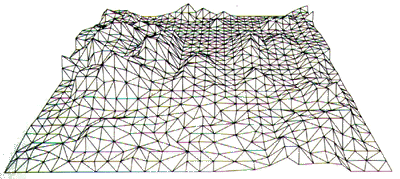
The problem consists of finding a way to represent relief on a map. A piece of
earth can be modeled as a terrain, which is a 2-dimensional surface in
3-dimensional space whith the property that every vertical line intersects it
in a point, if it intersects it at all. This model provides a good
representation only on a local scale, because the earth is round.
We can associate a function to this model, namely f:A included in R X R -> R
that assignes a height f(p) to every point p in the domain.

The problem is that we don't know the height of every point on earth, in other
words we know the value of function f only at a finite set of sample
points. We could assign for every known p the height of the nearest
point, but we would get a discrete terrain, which wouldn't look natural.
Another solution is to determine the triangulation of P, the set of
known points in the plan. Then, we can lift every point to it's correct height,
getting a polyhedral terrain, which can be used as an approximation for
the original terrain:

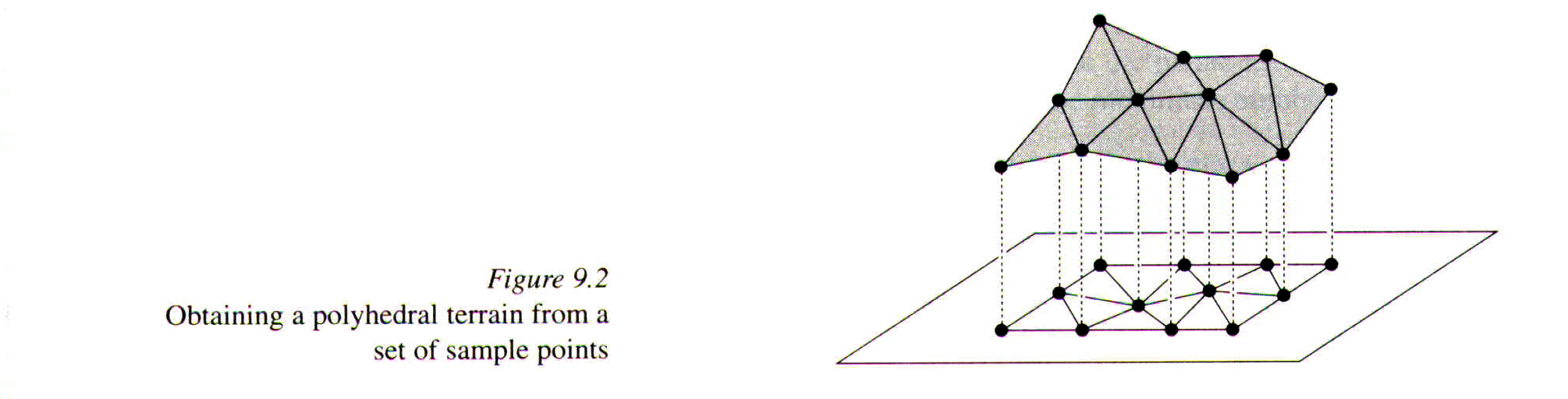
The question is how to triangulate the set of points. We do not know the original
terrain, we only know the sample points ant their heights. It might seem that any
triangulation is good, but some triangulations seem totaly different from others.
For example, in the following picture we can see the same set of points can
generate different triangulations:

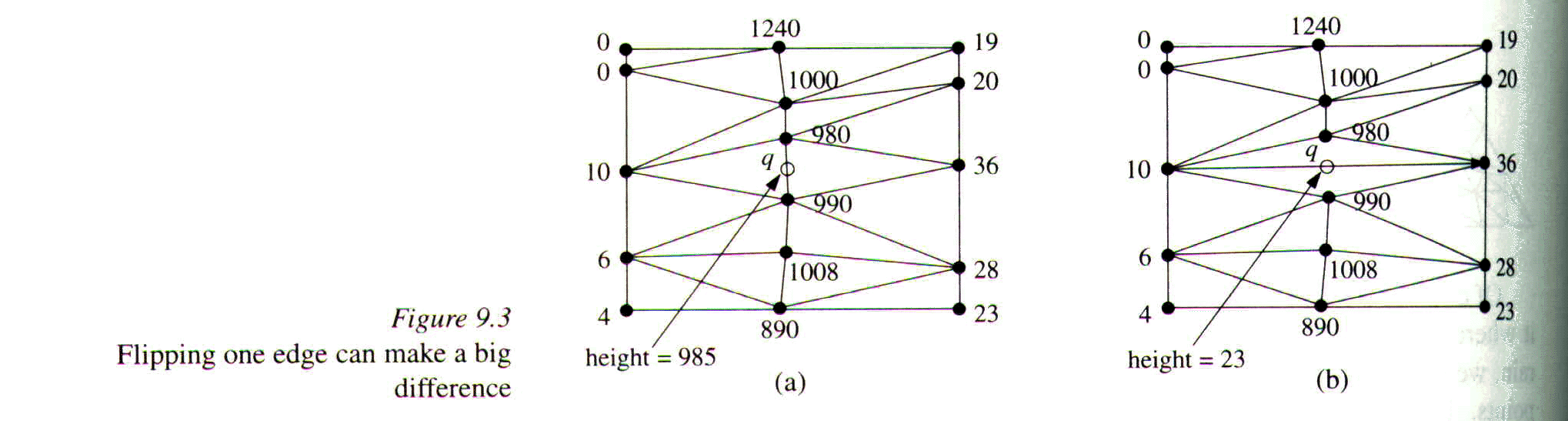
Triangulation a reflects the original terrain ( a mountain), while b
"introduces" narrow valleys cutting through the mountain ridge.
We can see that triangulation b is determined by 2 points that far away
from each other. We can also see that the angles are very small. We can therefore
rank triangulations by comparing their first angle, and eliminate the ones with
smaller angles. Since there is only a finite number of triangulations of a given
set P, there must be an optimal triangulation which maximizes the smallest angle.

Glossary of geometric terms


Key Words

Web Search Results

Bibliographic Search

Back
Last modified January 31, 1998, 10:11 PM.
Spent approximately 4 hours on this assignement.