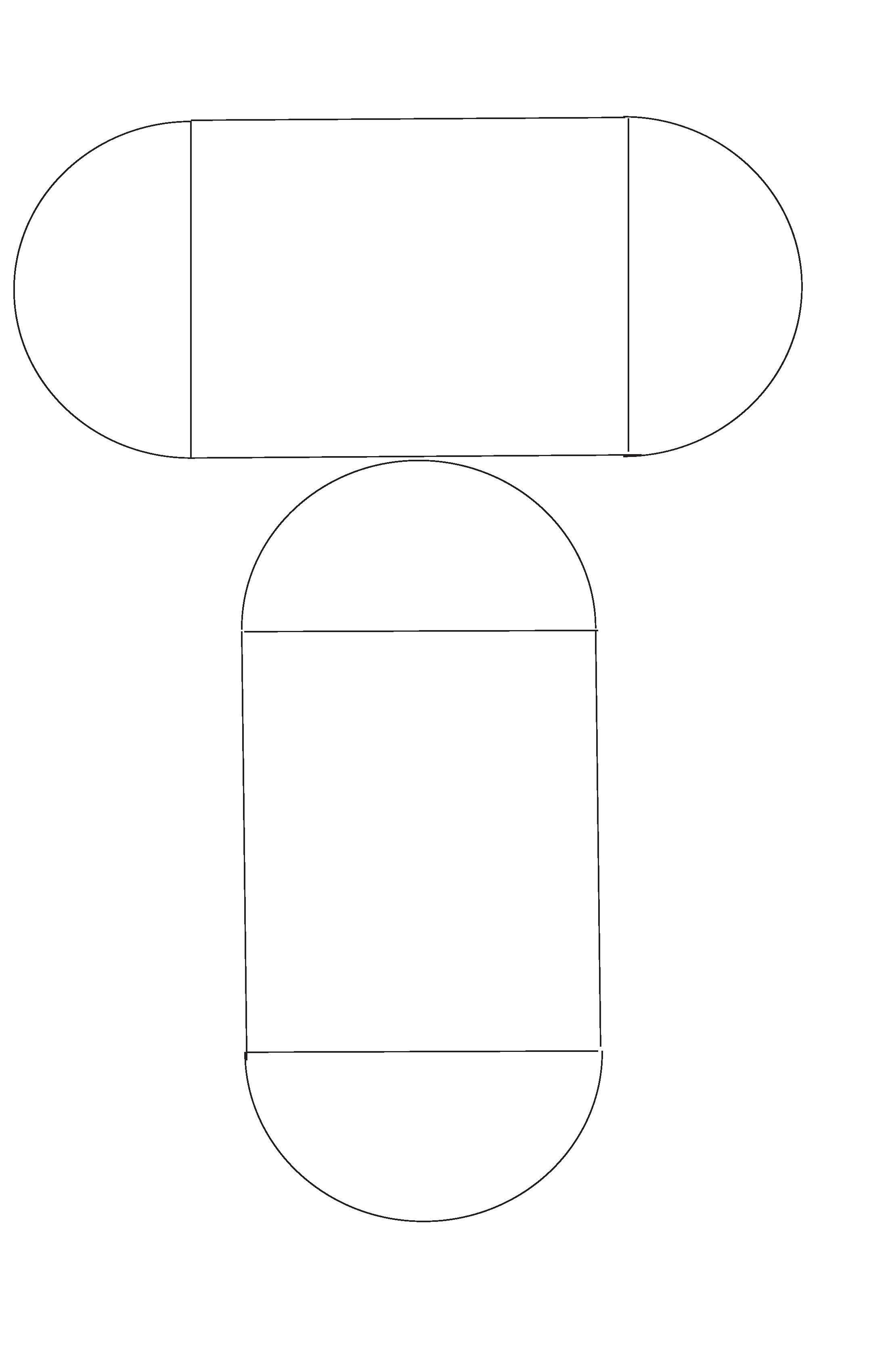
I worked with Stephanie Jakus and Professor O’Rourke on D-forms which are convex 3D objects constructed as follows. From two identical race-track shaped pieces of paper, we picked a random point on the edge of each. Then we glued these 2 points together, and “zipped” close the remainder of the race-track perimeters. The creased edge of this newly formed object is a closed curve in 3D that we have been studying. It is in general an unsolved problem to compute the shape of a D-form curve in space. The figure below (as shown to the right) shows the simplest D-form possible, where (as shown to the left) the midpoint of a circular arc of one racetrack is glued to the midpoint of one straight segment of the other racetrack.

We partitioned this curve into three parts: straight touching straight, curve touching straight, and curve touching curve. Using the definition of Gaussian curvature as angle deficit, we proved that the Gaussian curvature for straight-straight parts is 0. Because Gaussian curvature is intrinsic, we used a D-form that had no curve-curve part to study the curve-straight parts. We knew that integral of Gaussian curvature over the whole curve is 4 p by the Gauss-Bonnet theorem, and since there are four identical straight-curve parts, we concluded that the curvature for each point on those parts must be 1. Using the same logic combining with the notions of angle deficits, we also showed that the curvature at any point on the curve-curve parts must be 2. Thus we now know the distribution of Gaussian curvature over the whole surface, for it must be zero at every point not on the curve.

The straight-straight parts on D-forms lead us to question: if we glue two rectangular pieces of paper together along a common edge, does that edge have to be a straight line in space? We proved that that was the case when the tangent planes of the two surfaces of any point on that edge do not coincide.

(Supported by the National Science Foundation.)