What is the optimal partition of a square into convex pieces such that the circularity of the pieces is optimized? The circularity of a polygon is the ratio of the radius of its smallest circumscribing circle to the radius of its largest inscribed circle. Thus circular pieces have circularity near 1, and noncircular pieces have circularity greater than 1. An optimal partition minimizes the maximum ratio over all pieces in the partition.
Open.
This is a type of “fat” partition.
It is known from [DO03a] that the equilateral triangle requires an infinite number of pieces to achieve the optimal circularity of 1.5, and that for all regular k-gons, for k \ge 5, the one-piece partition is optimal. The square is a difficult intermediate case. It is known that the optimal ratio lies in the narrow interval [1.28868, 1.29950]. The upper bound is established by the 92-piece partition shown in Figure 1.
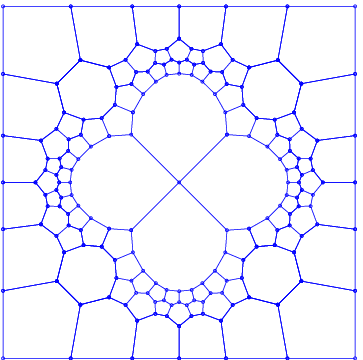
It is conjectured in [DO03a] that, as with the equilateral triangle case, no finite partition achieves the optimal ratio, but rather optimality can be approached as closely as desired as the number of pieces goes to infinity.
packing; meshing
J. O’Rourke, 16 Aug. 2004.