Icosamonohedra
(Becky Alexander and Joseph
O'Rourke)
 Below are the two icosamonohedra described in E. N. Miller's paper, "Icosahedra
Constructed from Congruent Triangles," Discrete and Computational Geometry
24: 437-451 (2000). An icosamonohedron is a polyhedron
topologically equivalent to an icosahedron (shown left), all of whose faces
are congruent triangles. Miller's paper constructs two examples.
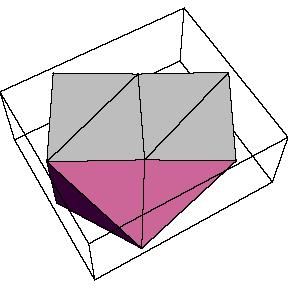
The first was discovered by Banchoff and Strauss in 1979. Its protoface
is a right triangle of side lengths {Sqrt[7], Sqrt[3], 2}. The polyhedron
is show in the top left figure below. Several triangles are coplanar,
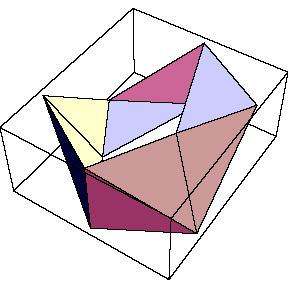
in groups of four, and of two. The figure to its right shows another
view of the polyhedron, with two opposite pentagons removed, leaving an
"equitorial band" of ten triangles.
Below are the two icosamonohedra described in E. N. Miller's paper, "Icosahedra
Constructed from Congruent Triangles," Discrete and Computational Geometry
24: 437-451 (2000). An icosamonohedron is a polyhedron
topologically equivalent to an icosahedron (shown left), all of whose faces
are congruent triangles. Miller's paper constructs two examples.
The first was discovered by Banchoff and Strauss in 1979. Its protoface
is a right triangle of side lengths {Sqrt[7], Sqrt[3], 2}. The polyhedron
is show in the top left figure below. Several triangles are coplanar,
in groups of four, and of two. The figure to its right shows another
view of the polyhedron, with two opposite pentagons removed, leaving an
"equitorial band" of ten triangles.
The second example constructed by Miller is new. Its protoface
is a nearly-right triangle of side lengths {3Sqrt[7], 2Sqrt[11],Sqrt[23]}.
The polyhedron is shown in the bottom left figure below, and again an equitorial
band is displayed to its right. Several pairs of adjacent triangles
are coplanar.
| Banchoff & Strauss polyhedron: |
Equitorial band of B & S's polyhedron: |
 |
 |
| Miller polyhedron: |
Equitorial band of Miller's polyhedron: |
 |
 |
It remains open to make a complete list of all icosamonohedra, as well
as to classify the combinatorial types of all monohedra.
 Below are the two icosamonohedra described in E. N. Miller's paper, "Icosahedra
Constructed from Congruent Triangles," Discrete and Computational Geometry
24: 437-451 (2000). An icosamonohedron is a polyhedron
topologically equivalent to an icosahedron (shown left), all of whose faces
are congruent triangles. Miller's paper constructs two examples.
The first was discovered by Banchoff and Strauss in 1979. Its protoface
is a right triangle of side lengths {Sqrt[7], Sqrt[3], 2}. The polyhedron
is show in the top left figure below. Several triangles are coplanar,
in groups of four, and of two. The figure to its right shows another
view of the polyhedron, with two opposite pentagons removed, leaving an
"equitorial band" of ten triangles.
Below are the two icosamonohedra described in E. N. Miller's paper, "Icosahedra
Constructed from Congruent Triangles," Discrete and Computational Geometry
24: 437-451 (2000). An icosamonohedron is a polyhedron
topologically equivalent to an icosahedron (shown left), all of whose faces
are congruent triangles. Miller's paper constructs two examples.
The first was discovered by Banchoff and Strauss in 1979. Its protoface
is a right triangle of side lengths {Sqrt[7], Sqrt[3], 2}. The polyhedron
is show in the top left figure below. Several triangles are coplanar,
in groups of four, and of two. The figure to its right shows another
view of the polyhedron, with two opposite pentagons removed, leaving an
"equitorial band" of ten triangles.



