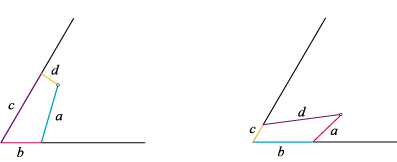Week 4:
Monday
This week we are starting to work in POV-Ray a little bit, experimenting with ways that we can create a good image displaying that the intersection of a sphere and a cone is a circle. We have figured out how to use the program on a basic level, enough so that we can make a transparent sphere (use the glass.inc package and choose a glass color). We have discovered that is actually difficult to design a clear image that displays this point though. In order to see the circle that is created, a camera must look at the cone dead on, but this is confusing because it does not really look like a cone. So we are still working on finding the optimal view.
Tuesday
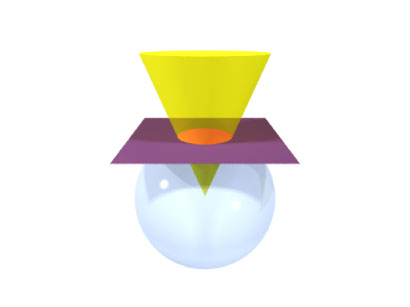
Today we finished our POV-ray figure of the cone intersecting the sphere. It came out pretty well, but we also learned a lot more about what can actually be accomplished in POV-ray, which made our accomplishment seem much less significant. We had some difficulties with getting the camera and the obejcts in the right place to create the picture we wanted. What we learned is that the coordinate system in POV-ray is very counter-intuitive, and that it is much easier to move your objects around the "world" than to move the camera so that it provides the desired view of the objects. The camera angle can be modified in many ways, but it is much harder to do this than to move the objects themselves. We also had some trouble getting the lighting to do what we wanted, because we were using simple spot lights which create a lot of contrast and strong shadows. This made our diagram a little hard to understand, so we ended up using so radiosity lighting that Joe had designed for another project, which looks much better. This is the code we used to create the lighting:
#declare RAD = on;
global_settings {
#if(RAD)
radiosity {
pretrace_start 0.08
pretrace_end 0.04
count 35
nearest_count 5
error_bound 1.8
recursion_limit 3
low_error_factor 0.5
gray_threshold 0.0
minimum_reuse 0.015
brightness 1
adc_bailout 0.01/2
}//radiosity
#end //if
}//global settings
We also used a few area lights, which produce softer shadows.
In order to create a sharp final image, we had to figure out how to use antialiasing in POV-ray. After doing a little searching around in the help menu, we found that you can manipulate antialiasing through the INI file settings. When you choose the Ini run setting, POV-ray gives you a number of options, including a command line where you can include different settings. In order to specify antialiasing, you can type either Antialias_Threshold=n.n or +An.n where n.n is a number between 0 and 1, which determines the level of antialiasing. n = 0.0 gives the highest quality. We discovered that you cannot just set n equal to 0, but must use the real number 0.0 in order for it to work. After all of this work, we also realized that the drop down menu of image rendering sizes that appears at the top left of the POV-ray screen allows you to select sizes with or without antialiasing, which allows you to turn antialiasing on without all of this work (although understanding how to manipulate the Ini settings is useful and gives you more control).
Wednesday
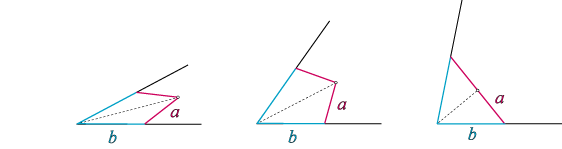
This morning I finished an example card I was making to show how v-folds can be used in the more artistic sort of card design that will be more often seen by children. It uses a sigle cut, creating two v-folds (one above the cut and one below it) to form the mouth of a bird. We will be taking pictures of this and a few other example cards later this week I think.
This afternoon we made a few quick diagrams for the document, and then worked on figuring out how to create animations with POV-ray. It turns out that it was not actually that difficult to do. We decided to practice animations by rotating the image of the intersection of the sphere and the cone we created yesterday 360 degrees in the plane orthogonal to the x axis. This produced an animation that shows the top and bottom views of the objects, which can make the circle of intersection clearer. In order to create this animation, we first created a union of all of the objects we wanted to rotate using the union command. Before closing the union, we used a rotate command to determine how we wanted the objects to move during our animation: rotate<-clock*360,0,0>. In order to create an animation, you must use the built-in clock variable somewhere in your code to determine the movement of your objects over time. There is a pretty good description of the variable if you search for "clock" in the help menu, but in order to understand this it is useful to first look at the INI options you must include for animations. If you select the Ini play option, above the command line there is a button allowing you to edit the specified INI settings. If you click on this, a window will open showing you the code that determines the settings for each size. You can change these settings to allow the creation of more than one image when you render your code. To do this, first find the setting you would like to use in the INI code. For example, for each image size there is a block of code that looks like this:
[160x120, No AA]
Width=160
Height=120
Antialias=Off
It specifies the image size and whether or not there will be antialiasing (AA). Find the block of code indicating the options you want to use for your animation. At the end of the code, add two new lines
Initial_Frame = 1
Final_Frame = 5
These new line specify the number of frames that you will to produce when you run your code. Here, we will create 5 separate images. The number of frames can be changed as desired. This relates to the clock variable, because clock represents a number between 0 and 1which is determined by the number of frames that you are using. This is a really nice feature, because POV-ray will divide the clock variable evenly between each of your frames, so that it increases at an even rate for each image you create. This means that when we rotated our objects by -clock*360 degrees in the x direction, our image was rotated by a different portion of the whole angle each time, creating a smooth animation.
In POV-ray, unfortunately, you cannot export a series of images into a GIF file the way you can on Mathematica. In order to string our individual BMP files into a GIF animation, we had to use outside software. I found a program with a free 30 day trial online that is pretty easy to use, called GIF Movie Gear. All I had to do was choose the "insert frames" option and import all of the BMP images that I wanted to include in the animation. The program does the rest--all you have to do is hit the play button and you can see your animation. We're going to try to play around with the software a bit over the next few days, to see if it is worth buying the real version, which costs about $40. We are also thinking about trying to create a POV-ray animation in an MPEG file, which would have much better quality, but is not quite as web-compatible. We'll have to see.
Thursday
Today we decided that there were a number of ways that our animation could be improved, so we modified it a bit, changing the colors and dimensions to better prove our point. The final product is looking pretty nice. Did I mention that I love POV-ray?
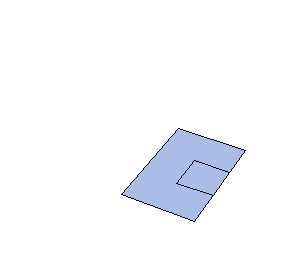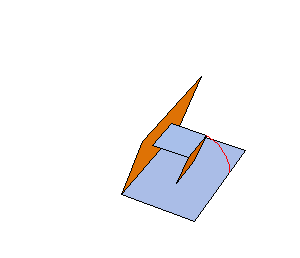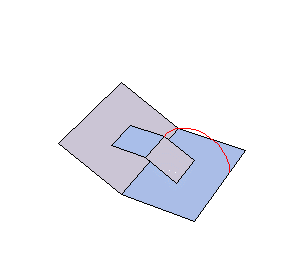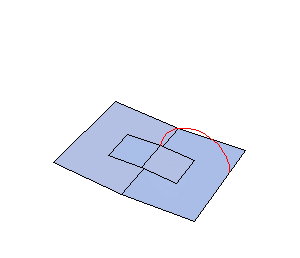
Next we started working on an animation that will display the intersection of the cone with the median plane of a rotary motion pop-up card. Didn't get too far.
Friday
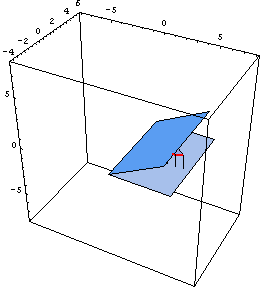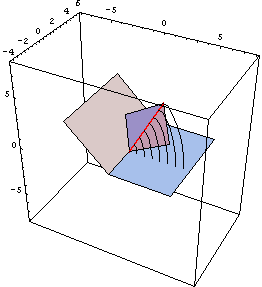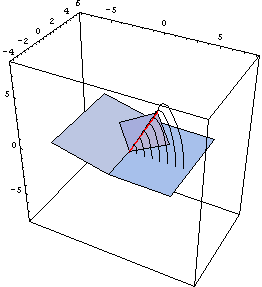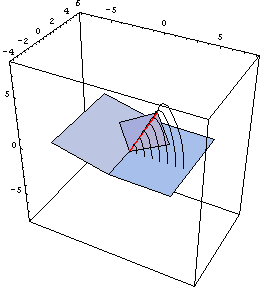
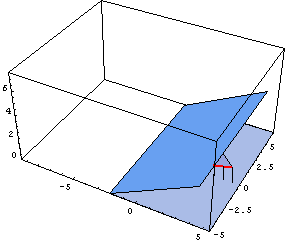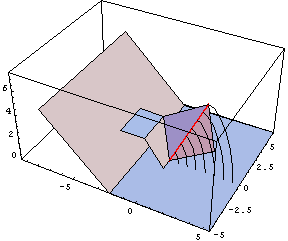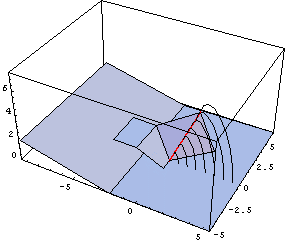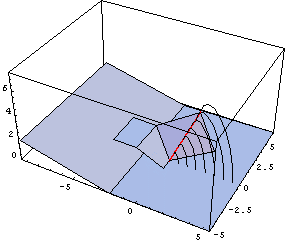
Today we worked on the median plane animation in POV-ray, and had a lot of difficulty describing the creation of the circle that traces the intersection of the median plane and the cone. What we want our animation to show is that as the median plane moves through the cone defined by the rotary motion of the v-fold, the intersection is a quarter-circle (or wedge, if you look at the entire intersection). In order to animate this in POV-ray, we must use the intersection of a thin torus and a wedge-shaped prism to draw something that looks like a portion of a circle on the median plane. This coordinates of the wedge were a little tricky to find, but our main problem now is that we cannot find the angle that determines how much of the circle should be drawn at each point in time. Initially, we thought that the quarter circle would be drawn at a constant rate, but it appears that this is not actually true. We cannot see how the rate of change of this anlge relates to anything else in our scenario, so we haven't yet been able to produce an accurate animation. |