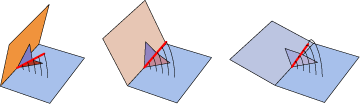
Fig. 1
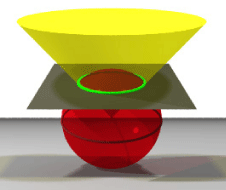
Fig. 2
Cone/Sphere Intersection in a Pop-Up Card Design
Ana Spasova
This summer I worked with Nell O’Rourke and Faith Weller on a Pop-Up Cards project. The goal was to help Professor O’Rourke with the guide that he is writing called Pop-Up Card Design as a Vehicle to Teach Mathematics. Our project was divided into three major areas: Parallel Folds, Angle Folds, and Rotary Motion. For each part we designed pop-up cards and wrote Mathematica code to animate them. The basic process that we followed for each card was the following: we created variables for the different geometric parts of the card; then we built our card by defining various polygons and putting them together; at the end, we showed the whole array of images to finally get our animations.
Fig. 1 |
Fig. 2 |
One of the more complicated cards that we worked on was the V-fold card. The simplest V-fold card produces a cone when it opens (Fig.1 above). Our goal was to illustrate that this cone and a sphere that is centered at the tip of the cone intersect in a circle. The motion of this simple V-fold depends on the understanding exactly how this circle is exactly produced. After starting to write the section on this card we realized that it would be difficult to illustrate this point without providing an image that clearly displays the intersected circle. Using POV-ray we created a transparent cone and a sphere, and animated the image to represent this concept more clearly (Fig. 2 above).
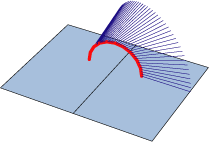 |
The V-fold card turned out to be more complicated and intriguing than we originally thought. First, the side tip of the V-fold moves on a circle, which we know because the V-fold is produced by a single cut of the card. If we extend the side tip of the V-fold with a segment attached to the V, this segment moves in a complicated way when the card opens. After we plotted the surface in Mathematica we found that there is no apparent regularity to the surface, as you can see in the figure to the left. The shape that the extended side tip of the V-fold traces in space does not seem to lie in a plane. The shape, although not regular, is a very elegant one. We only know that it is a “ruled surface.” |
(Supported by the National Science Foundation.)
Advisor: Joseph O’Rourke