
The generalization of this lemma permits opening of the angles beyond pi, as far reflex as they were originally convex. The conclusion remains the same: e cannot shorten.
This theorem can be derived from Chern's proof1 of a theorem of Axel Schur2, employing differential geometry, or, independently, by induction [O'R00].

The turn angle ranges are displayed in green, and the "forbidden shoulder circle" is drawn in blue. The user may then turn any joint of the chain by double-clicking on it and dragging the next link,
which rotates the (red) subchain beyond that link as rigid unit:
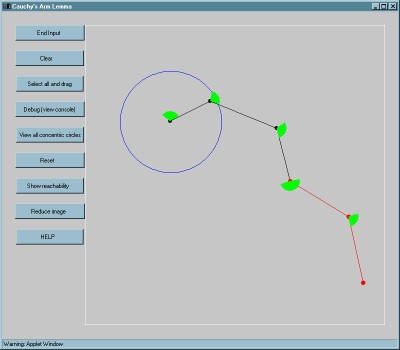
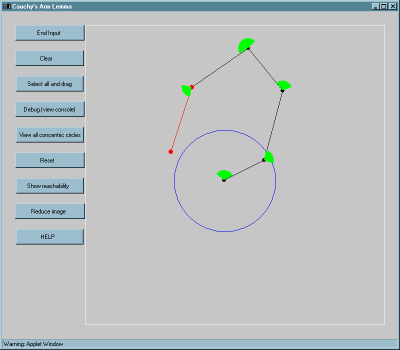
The theorem says that no reconfiguration within the allowable turn angle ranges will permit the hand to enter the forbidden circle:
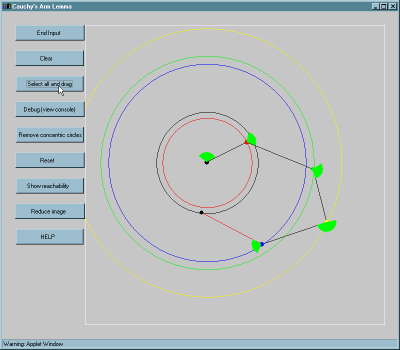
A corollary says that every joint has a correspoding forbidden circle, which can be viewed by selecting:View all concentric circles
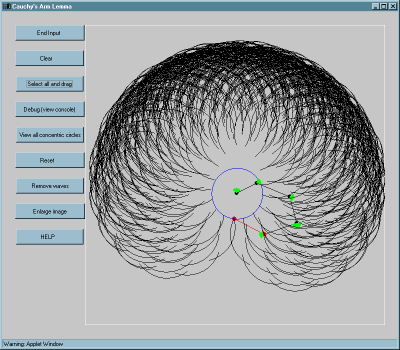
For more details, see the paper [O'R00].
| Platform | OS | Browser | |
| Internet Explorer | Netscape Communicator | ||
| PC | Windows 9x, WindowsNT4 | IE v4: No reported problems at above resolutions. | NC v4.7: No reported problems on above resolution. |
| Red Hat Linux 6.1 | Not tested. | Netscape v4.61 for Linux. No reported problems. | |
| MAC | MacOS 8.5 | IE v4: No reported problems at above resolutions. | Some Mac versions of Netscape do not support the Java1.2 event model, which is used extensively on the applet. Therefore, IE is recommended for the Mac |
| SGI | Irix 6.x | Not tested. | Tested on Netscape 4.07. Reported problems are:
|