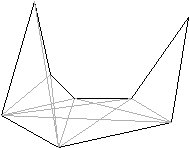
As described in previous sections, our O(n log n) algorithm does not find the optimal/shortest path. To find the optimal path, we need a tool called the visibility graph. The visibility graph of a polygon is a graph whose nodes corresponds to the vertices of the polygon, and whose edges correspond to the edges in the polygon formed by joining the vertices that can “see” each other. The figure below shows the visibility graph of the polygon.


A Java applet computing the visibility graphs of polygons and sets of obstacles has been implemented. It can be found at http://hamp.hampshire.edu/~ppk96/cg/mApplet.html
To compute the visibility graph of a polygon, click points on the interface and choose Compute, Visibility Graph, Polygon, Naïve Alg. This will give you the internal visibility edges. If you want the external visibility edges instead, choose Compute, Visibility Graph, Polygon, External edges, and then click one more point. You will see the external visibility edges.
Computing
the visibility graph of a set of obstacles involves a slightly more complicated
procedure. This is because you will need to tell the program which point
sets define an obstacle. Moreover, you will want to have the obstacles
filled with a color, so that the visibility edges will be more obvious.
First, choose Compute, Visibility Graph, Obstacles, Fill Polygons.
Then choose Compute, Visibility Graph, Polygon, Naïve Alg.
Then click points on the interface which are the vertices of your first
obstacle. After clicking all points belonging to the first obstacle, choose
Compute, Visibility Graph, Polygon, Define Polygon. You will then
see the first obstacle filled and bounded by a black boundary. Now you
should click points that will be the vertices of the second obstacle. After
you have finished, choose Compute, Visibility Graph, Polygon, Define
Polygon. Again the second obstacle will be defined, and the visibility
edges between the first and second obstacles will also be computed. Repeat
the process for additional obstacles. If you do not want the obstacles
filled, then omit the first step on Fill Polygons.
Why do Visibility Graphs give the shortest path?
Lemma : Any shortest path between pstart and pgoal among a set S of disjoint polygonal obstacles is a polygonal path whose inner vertices are vertices of S.
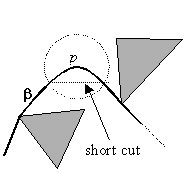
Proof by contradiction. Suppose there is a shortest path B that is not polygonal, as shown in the diagram above. We take point p on B. Since p is in the interior of the free space, there is a disc of positive radius centered at p that is completely contained in the free space. The part of B inside the disc, which is not a straight line segment, can be shortened by replacing it with a straight line connecting the two points where B enters the disc and leaves the disc. This contradicts the assumption that B is a shortest path, since any shortest path must be locally shortest, that is, any subsections of a shortest path must itself be the shortest path of that section.
By this Lemma, the segments on a shortest path are visibility edges, except for the first and last segment. To make them visibility edges as well, we add the start and goal position as vertices to S. With this visibility graph as our road map, we can now determine the shortest path by single-source shortest path algorithms. We will return to an example of such an algorithm, Dijkstra’s algorithm, after presenting algorithms for computing visibility graphs.
Algorithms for Computing Visibility Graphs of Obstacles
Input: a set of points defining the obstacles.
Output: a set of points which correspond to the visibility
edges of the obstacles
Several algorithms exist with different time complexities.